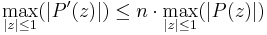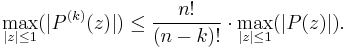Bernstein's inequality (mathematical analysis)

In mathematical analysis, Bernstein's inequality is named after Sergei Natanovich Bernstein. The inequality states that on the complex plane, within the disk of radius 1, the degree of a polynomial times the maximum value of a polynomial is an upper bound for the similar maximum of its derivative.

Theorem

Let P be a polynomial of degree $n$ on complex numbers with derivative P′. Then

$\max_{|z| \le 1}( |P'(z)| ) \le n\cdot\max_{|z| \le 1}( |P(z)| )$

The inequality finds uses in the field of approximation theory.

Using the Bernstein's inequality we have for the k:th derivative,

$\max_{|z| \le 1}( |P^{(k)}(z)| ) \le \frac{n!}{(n-k)!} \cdot\max_{|z| \le 1}( |P(z)| ).$

References

C. Frappier, Note on Bernstein's inequality for the third derivative of a polynomial, Journal of Inequalities in Pure and Applied Mathematics, Vol. 5, Issue 1, Article 7, 6 pp., 2004. [1]

‹The stub template below has been proposed for renaming to . See stub types for deletion to help reach a consensus on what to do.
Feel free to edit the template, but the template must not be blanked, and this notice must not be removed, until the discussion is closed. For more information, read the guide to deletion.›

Bernstein's inequality (mathematical analysis)

Theorem

See also

References